тюет«їТѕљу░Атќ«уџёOpenMPТИгУЕдтЙї№╝їТјЦСИІСЙєСй┐ућет░ѕжќђућеСЙєТИгУЕдТх«ж╗ъжЂІу«ЌУЃйжЄЈуџёуеІт╝Јуб╝СЙєТИгУЕдтќ«СИђС╝║ТюЇтЎеуџёжЂІу«ЌУЃйжЄЈ№╝їСИ╗УдЂТИгУЕдNetlibТЈљСЙЏуџёHPL№╝їС╗ЦтЈіNASAТЈљСЙЏуџёNPB№╝їжђЈжЂјжђЎтЁЕтђІтцДтъІуџёТИгУЕдуеІт╝Јуб╝№╝їтЈ»С╗ЦУ«ЊУ«ђУђЁТЏ┤тіаС║єУДБТГцТгЙС╝║ТюЇтЎеуџёжЂІу«ЌТЋѕУЃйсђѓ
Part3 жђ▓жџјт╣│УАїТЋѕУЃйТИгУЕд
1000dТИгУЕд
1000dуџёТИгУЕдуеІт╝Јуб╝тЈ»С╗ЦтЙъNetlibуџёуХ▓уФЎСИіСИІУ╝Ѕ(http://www.netlib.org/benchmark/1000d)№╝ї жђЎтђІуеІт╝ЈСИ╗УдЂТў»Т▒ѓУДБуиџТђДУЂ»уФІТќ╣уеІт╝ЈуџёТЋИтђ╝УДБ№╝їС┐ѓТЋИуЪЕжЎБуѓ║1000X1000№╝їТ▒ѓУДБТќ╣т╝ЈТў»Сй┐ућежФўТќ»ТХѕтј╗Т│Ћ(Gaussian elimination with partial pivoting)№╝їУЌЅућ▒ТИгжЄЈуеІт╝ЈтЪиУАїуџёТЎѓжќЊтЈЇу«ЌУЎЋуљєтЎеуџёТх«ж╗ъжЂІу«ЌТЋѕУЃй№╝їТЋѕУЃйтќ«СйЇтљїТеБуѓ║Mflops№╝їТ»ЈуДњтЪиУАїСИђуЎЙУљгТгАТх«ж╗ъжЂІу«Ќ№╝їТюгТИгУЕдСй┐ућеIntel Fortran 9.1уиеУГ»тЎе№╝їуиеУГ»жЂИжаЁуѓ║-fast№╝їТИгтЄ║СЙєуџёухљТъюуѓ║738Mflops№╝їуЎ╝ТЈ«СИЇтѕ░УЎЋуљєтЎетЇЂтѕєС╣ІСИђуџёУеѕу«ЌУЃйжЄЈсђѓ
тдѓТъюУ«ђУђЁТюЅУѕѕУХБтЈ»С╗ЦУЕдУЉЌт░Є1000d.fуеІт╝Јуб╝С┐«Тћ╣ТѕљтЉ╝тЈФLapackуџётЄйт╝ЈСИдСИћжђБухљтѕ░Intel Math Kernel Library(MKL)№╝їТюЃуЎ╝уЈЙТИгтЄ║СЙєуџёухљТъюТюЃтцДт╣ЁуџёТѕљжЋи№╝їжђЎТў»тЏауѓ║MKLти▓уХЊжЄЮт░ЇУЎЋуљєтЎеуџёт┐ФтЈќУеўТєХжФћУѕЄуАгжФћТъХТДІтЂџжЂјТюђСй│тїќ№╝їтЏаТГцтЈ»С╗ЦуЎ╝ТЈ«СИЃтѕ░тЁФТѕљуџёУЎЋ уљєтЎеТх«ж╗ъжЂІу«ЌТЋѕУЃй№╝їС┐«Тћ╣уџёТќ╣т╝ЈСИдСИЇтЏ░жЏБ№╝їтЈфУдЂт░ЄуеІт╝Јуб╝УБАуџёуЪЕжЎБтѕєУДБdgefaТћ╣ТѕљтЉ╝тЈФdgetrf№╝їТюфуЪЦТЋИТ▒ѓУДБтЙъdgeslТћ╣ТѕљтЉ╝тЈФdgetrsт░▒тЈ»С╗Ц№╝ї уеІт╝Јуб╝тдѓСИІсђѓ
тјЪтДІуеІт╝Јуб╝:
| call dgefa(a,lda,n,ipvt,info) call dgesl(a,lda,n,ipvt,b,0) |
С┐«Тћ╣уеІт╝Јуб╝:
| call dgetrf(n,n,a,lda,ipvt,info) call dgetrs(’N',n,1,a,lda,ipvt,b,lda,info) |
С╣ІтЙїуиеУГ»тЄ║тЪиУАїТфћ№╝їтЪиУАїтЅЇтЁѕТїЄт«џтЈфУдЂСй┐ућеСИђтђІтЪиУАїуињСЙєУеѕу«Ќ№╝їтЏауѓ║MKLС╣ЪТў»Сй┐ућетѕ░OpenMPуџёТќ╣т╝ЈСЙєжђ▓УАїт╣│УАїУеѕу«Ќ№╝їТЅђС╗ЦтЈ»С╗ЦућеСИІжЮбуџёТїЄС╗цСЙєУеГт«џуњ░тбЃУ«іТЋИТјДтѕХтЪиУАїуињуџёТЋИуЏ«сђѓ
export OMP_NUM_THREADS=1
уёХтЙїтЪиУАїуеІт╝Ј№╝їтЈ»С╗ЦУиЉтЄ║6.9Gflops(1Gflops = 1000MFlops)уџёухљТъю№╝їТЋѕУЃйТѕљжЋи9тђЇтцџ№╝їтдѓТъют░ЄуЪЕжЎБтцДт░ЈУф┐ТЋ┤тѕ░12000X12000№╝їС╗ЦтЈітбътіатЪиУАїуињуџёТЋИуЏ«№╝їтЈ»С╗ЦТИгтЄ║ТЏ┤жФўуџёТѕљуИЙ№╝їтдѓСИІУАесђѓ
| тЪиУАїуињТЋИуЏ« | GFlops | Speedup | Efficiency(%) |
| 1 | 8.88 | 1 | 100 |
| 2 | 17.02 | 1.92 | 96 |
| 4 | 28.65 | 3.23 | 80.7 |
| 8 | 35.74 | 4.02 | 50.3 |
ућ▒ТИгУЕдуџёТЋИТЊџтЈ»С╗ЦуюІтЄ║СЙє№╝їжђЎТгЙтЏЏТаИт┐ЃС╝║ТюЇтЎетюетЁЕтђІтЪиУАїуињуџёТЃЁТ│ЂСИІжђЪт║дТѕљжЋиТјЦУ┐ЉтЁЕтђЇ№╝їСИЇжЂјжџеУЉЌтЪиУАїуињТѕљжЋитѕ░4Тѕќ8тђІТЎѓ№╝їт╣│УАїТЋѕуЏіжЎЇтѕ░80%тњї50%№╝їСИ╗УдЂтјЪтЏажѓёТў»тюеТќ╝жђЎтЈ░ТЕЪтЎеуџёУеўТєХжФћтГўтЈќСИдСИЇТў»ТюђСй│уџёУеГт«џ№╝їтЏаТГцуЋХтЪиУАїуињтбътіа№╝їСИ╗УеўТєХжФћуџёжа╗т»гт░▒СИЇУХ│№╝їжђаТѕљТЋѕУЃйТЈљтЇЄуџёуЊХжаИсђѓ
тдѓТъюУ«ђУђЁжђ▓УАїуџёТЋИтђ╝Уеѕу«ЌУБАТюЅСй┐ућетѕ░LapackуџётЄйт╝Ј№╝ї тюеТљГжЁЇMKLС╗ЦтЈіжђЎТгЙтЏЏТаИт┐ЃС╝║ТюЇтЎе№╝їтЈ»С╗ЦтюеСИЇућеТњ░т»Фт╣│УАїУеѕу«ЌуеІт╝ЈСИІ№╝їтцДт╣ЁТЈљтЇЄУеѕу«ЌуџёжђЪт║д№╝їУђїжђЎжАєтЏЏТаИт┐ЃУЎЋуљєтЎетњїС╗ЦтЙђXeonУЎЋуљєтЎеуЏИТ»ћУ╝Ѓ№╝їСИђжаЁтЙѕтцДуџётёфтІб уѓ║Т»ЈтђІТаИт┐ЃжЃйтЁиТюЅуЇеуФІтЪиУАїSSEТїЄС╗цуџётіЪУЃй№╝їСИЇТюЃуЎ╝ућЪС╗ЦтЙђСй┐ућеHyper-ThreadingТЎѓтЁЕтђІтЪиУАїуињУ╝фТхЂСй┐ућеSSEТїЄС╗цуџёуЏ▓ж╗ъсђѓ
HPLТИгУЕд
HPLТў»СИђтЦЌТИгУЕдтѕєТЋБт╝ЈУеўТєХжФћуњ░тбЃуџёТх«ж╗ъжЂІу«ЌТЋѕУЃйтиЦтЁи№╝їжђЈжЂјжђЎухёуеІт╝Јуб╝тЈ»С╗ЦТИгжЄЈтЄ║тЈбжЏєу│╗ух▒(Cluster)уџёт╣│УАїУеѕу«ЌУЃйжЄЈ№╝їTop500уџёТЋѕУЃйТЋИТЊџТИгУЕдС╣ЪТў»С╗ЦHPLуѓ║тЪ║Т║ќ№╝їу░Атќ«СЙєУгЏHPLтЈ»С╗ЦУдќуѓ║1000dуџёMPIуЅѕТюг№╝їHPLтљїТеБтЈ»С╗ЦтЙъNetlibСИіСИІУ╝Ѕhttp://www.netlib.org/benchmark/hpl/№╝їУДБжќІтЙїжюђУдЂуиеУ╝»Makefile(Make.Clovertown)УеГт«џуиеУГ»тЈЃТЋИ№╝їжђЎТгАуџёТИгУЕдТюЅСй┐ућетѕ░MKLуџётЄйт╝Јт║Ф№╝їуиеУГ»тЄ║тЪиУАїТфћ(xhpl)тЙї№╝їтЈ»С╗ЦжђЈжЂјуиеУ╝»У╝ИтЁЦТфћТАѕ(HPL.dat) СЙєТјДтѕХС┐ѓТЋИуЪЕжЎБтцДт░ЈС╗ЦтЈіуЏИжЌют╣│УАїУеѕу«ЌУеГт«џ№╝їтЏауѓ║MKLТюгУ║ФтЈ»С╗ЦУеГт«џтЪиУАїуињуџёт╣│УАїУеѕу«Ќ№╝їтЏаТГцтюеТИгУЕдТЎѓжюђУдЂуЅ╣тѕЦТїЄт«џOMP_NUM_THREADSуџёуњ░тбЃУ«і ТЋИ№╝їтдѓТъюТ▓њТюЅТїЄт«џ№╝їMKLжаљУеГТюЃСй┐ућетѕ░у│╗ух▒уџёТЅђТюЅУЎЋуљєтЎеУ│ЄТ║љ№╝їТюЃжђаТѕљтњїMPIТљХСйћУЎЋуљєтЎеуџёуІђТ│Ђ№╝їт»джџЏТљГжЁЇMPIуџёТИгУЕдухётљѕт░▒тЙѕтцџуе«№╝їТИгУЕдТЋИТЊџтдѓСИІУАе№╝їтќ«СйЇ уѓ║GFlops№╝їТ»ЈуДњтЪиУАїтЇЂтёёТгАТх«ж╗ъжЂІу«Ќсђѓ
| Np | Thread=1 | Thread=2 | Thread=4 | Thread=8 |
| 1 | 8.89 | 17.01 | 29.04 | 31.3 |
| 2 | 16.73 | 8.63 | 30.8 | |
| 4 | 26.82 | 29.3 | ||
| 8 | 28.95 |
СИіУАеуџёТЋИТЊџСИГNpС╗БУАеNumber of Process№╝їтдѓТъюСй┐ућетѕ░тЁФтђІТаИт┐ЃСЙєУеѕу«Ќ№╝їт░▒ТюЃТюЅтЏЏуе«ухётљѕТќ╣т╝Ј№╝їТЋѕУЃйТюђСй│уџёТў»Np=1,Thread=8жђЎухё№╝їТюђти«уџёТў»Np=8,Thread=1№╝їтјЪ тЏатюеТќ╝NpТЋИуЏ«УХітцџжюђУдЂтѕЄтЅ▓уџёуЪЕжЎБт░▒УХітѕєТЋБ№╝їУ│ЄТќЎС║цТЈЏжюђУдЂуџёТЎѓжќЊТЏ┤тцџ№╝їтЏаТГцТюЃтй▒жЪ┐тѕ░Уеѕу«ЌуџёТЋѕУЃйсђѓтдѓТъютѕєТъљThread=1ТЃЁТ│ЂСИІуџёSpeedтњї Effiency№╝їтдѓСИІУАеТЅђуц║№╝їТюЃуЎ╝уЈЙТюђТюЅТЋѕујЄуџёухётљѕТў»Np=4жђЎухёТЋИТЊџ№╝їжђЪт║дтЈ»С╗ЦТЈљтЇЄ3.02тђЇ№╝їжЂћтѕ░75.5%уџёт╣│УАїтїќТЋѕуЏісђѓ
| Np | Thread=1 Speedup | Thread=1 Effiency(%) |
| 1 | 1 | 100 |
| 2 | 1.88 | 94 |
| 4 | 3.02 | 75.5 |
| 8 | 3.26 | 40.75 |
NPBТИгУЕд
NPBТў»ућ▒NASAТЅђТјетЄ║уџёУеѕу«ЌТхЂжФћтіЏтГИ(CFD)ТЋѕУЃйТИгУЕдуеІт╝Јуб╝№╝їNPBтЁетљЇуѓ║NAS Parallel Benchmarks№╝їNASтЅЄТў»NASA Advanced SupercomputingуџёуИ«т»Ф№╝їNPBтїЁтљФС║ћухёТЋИтђ╝Уеѕу«ЌуеІт╝ЈтњїСИЅухёCFDТЄЅућеуеІт╝Ј№╝їУЌЅућ▒жђЎС║ЏуеІт╝ЈтЈ»С╗ЦТИгУЕдтЄ║Уеѕу«ЌтЈбжЏєуџёТх«ж╗ъжЂІу«ЌТЋѕУЃй№╝їТюгТгАТИгУЕдућеуџёТў» NPB 3.0уЅѕТюг№╝їТГцуЅѕТюгжЎцС║єжЄЮт░ЇтјЪТюЅуџётЙфт║ЈуеІт╝Јжђ▓УАїТюђСй│тїќУф┐ТЋ┤тцќ№╝їжѓёТћ»ТЈ┤OpenMPуџётіЪУЃй№╝їтЏаТГцтЈ»С╗ЦућеСЙєТИгУЕдтцџТаИт┐ЃуџёС╝║ТюЇтЎе№╝їуеІт╝Јуб╝уџёСИІУ╝ЅУФІтЈЃУђЃуХ▓жаЂСИіуџёТїЄ уц║(http://www.nas.nasa.gov/Resources/Software/npb.html)тдѓТъюУ«ђУђЁТ▓њТюЅNASуџётИ│УЎЪжюђУдЂуиџСИіУе╗тєітЙїТЅЇУЃйСИІУ╝ЅуеІт╝Јуб╝сђѓ
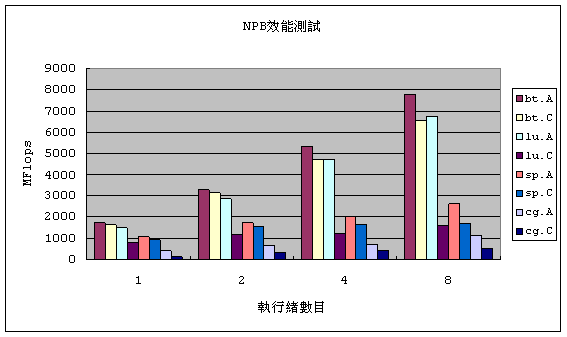
NPBТИгУЕдтЈ»С╗ЦТїЄт«џуЪЕжЎБуџётцДт░Ј№╝їтЁ▒тѕєТѕљSсђЂWсђЂAсђЂBсђЂCтњїDтЁГуе«уГЅу┤џ№╝їТюгТгАТИгУЕдСИ╗УдЂС╗ЦAтњїCуѓ║СИ╗№╝їуХ▓Та╝тцДт░ЈтѕєтѕЦуѓ║64*64*64тњї162*162*162№╝їТЋИТЊџуџёТЋ┤уљєС╗ЦbtсђЂluсђЂspтњїcgжђЎтЏЏуе«ТИгУЕдуеІт╝Јуб╝уѓ║СИ╗№╝їС╗ЦСИІу»ђжїёNPBуџёуеІт╝Јуб╝С╗Іу┤╣сђѓ
- BT is a simulated CFD application that uses an implicit algorithm to solve 3-dimensional (3-D) compressible Navier-Stokes equations. The finite differences solution to the problem isbased on an Alternating Direction Implicit (ADI) approximate factorization that decouplesthe x, y and z dimensions. The resulting systems are Block-Tridiagonal of 5×5 blocks and are solved sequentially along each dimension.
SP is a simulated CFD application that has a similar structure to BT. The finite differences solution to the problem is based on a Beam-Warming approximate factorization that decouples the x, y and z dimensions. The resulting system has Scalar Pentadiagonal bands of linear equations that are solved sequentially along each dimension.LU is a simulated CFD application that uses symmetric successive over-relaxation (SSOR) method to solve a seven-block-diagonal system resulting from finite-difference discretization of the Navier-Stokes equations in 3-D by splitting it into block Lower and Upper triangular systems.CG uses a Conjugate Gradient method to compute an approximation to the smallest eigenvalue of a large, sparse, unstructured matrix. This kernel tests unstructured grid computations and communications by using a matrix with randomly generated locations of entries.
NPBуџёТх«ж╗ъжЂІу«ЌТИгУЕдухљТъютдѓСИІтюќТЅђуц║№╝їућ▒тюќСИіСЙєуюІС╗ЦbtуџёТх«ж╗ъжЂІу«ЌТЋИтђ╝ТюђжФў№╝їтЁХТгАТў»luтњїsp№╝їcgТИгУЕдтЄ║СЙєуџёухљТъюТюђти«сђѓ
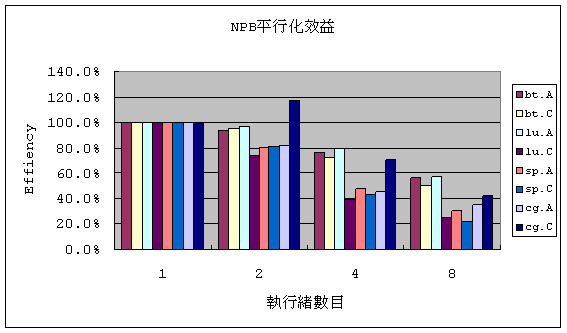
тдѓТъют░ЄТЋИТЊџУйЅТѕљућеEffiencyСЙєуюІ№╝їтдѓСИІтюќТЅђуц║№╝їС╗Цbt.AуџёТЃЁТ│ЂСЙєуюІ№╝їтЈ»С╗ЦуЎ╝уЈЙуЋХтЪиУАїуињуѓ║2тђІТЎѓжѓётЈ»С╗ЦуХГТїЂтюе94.5%уџёт╣│УАїтїќТЋѕуЏі№╝їуЋХтЪиУАї уињуѓ║4 тђІТЎѓжЎЇтѕ░76.9%№╝їтбътіатѕ░8тђІтЪиУАїуињТЎѓжЎЇтѕ░56.1%№╝їтЈдтцќтЈ»С╗ЦуюІтЄ║btсђЂluтњїspжђЎСИЅтђІCFDУеѕу«ЌуеІт╝ЈС╗ЦspуџёТ╝ћу«ЌТ│ЋТюђСИЇжЂЕтљѕжђ▓УАїт╣│УАїУеѕу«Ќ№╝їluтЅЄ Тў»уЋХуХ▓Та╝ТѕљжЋитѕ░CуГЅу┤џТЎѓ№╝їт╣│УАїТЋѕуЏіжЎЇуѓ║СИђтЇі№╝їbtуџёТ╝ћу«ЌТ│ЋтЅЄтюеAтњїCуГЅу┤џжЃйуХГТїЂСИђТеБуџёт╣│УАїтїќТЋѕуЏі№╝їтјЪтЏатЈ»С╗ЦтюеТќ╝luтњїspжђЎтЁЕуе«Т╝ћу«ЌТ│Ћт░ЇТќ╝уХ▓Та╝уџётГўтЈќТ»ћжЄЇ Т»ћУ╝ЃжФў№╝їТЅђС╗Цт░ЇТќ╝УеўТєХжФћуџёжа╗т»гУдЂТ▒ѓуЏИт░ЇТ»ћbtжѓёжФў№╝їтЏаТГцТх«ж╗ъжЂІу«ЌТЋѕУЃйтюет╣│УАїтїќуџёТЃЁТ│ЂСИІТЈљтЇЄТюЅжЎљсђѓ
ухљУФќ
тюеуЈЙС╗іУЎЋуљєтЎеТюЮтљЉтцџТаИт┐ЃуџёТъХТДІуЎ╝т▒ЋуџёУХетІбСИІ№╝їтдѓТъюТЃ│УдЂтюежђЎТеБуџёуњ░тбЃСИІтіат┐ФУеѕу«ЌуџёжђЪт║д№╝їт░▒т┐ЁжаѕС║єУДБтцџТаИт┐ЃТъХТДІСИІуџёТЋѕУЃйуЊХжаИуѓ║СйЋ№╝їтюеТюгТгАТИгУЕдСИГ№╝їтЈ»С╗Ц тцДуЋЦтѕєТѕљтЁЕжАъуџёУеѕу«ЌуеІт╝Ј№╝їуггСИђжАъТў»тќ«у┤ћтцДжЄЈуџёТЋИтђ╝Уеѕу«Ќ№╝їтдѓMolecular dynamics simulationТИгУЕд№╝їућетѕ░8тђІТаИт┐ЃтљїТЎѓУеѕу«Ќ№╝їжђЪт║дтЈ»С╗Цт┐Фу┤ё7.6тђЇ№╝їжЂћтѕ░96%уџёт╣│УАїтїќТЋѕуЏі№╝їуггС║їжАъТў»Уеѕу«ЌжЂјуеІСИГТюЃтГўтЈќтцДжЄЈУеўТєХжФћуџёуеІт╝Ј№╝їтдѓHPL тњїNPBуГЅ№╝їТГцТЎѓт░▒ТюЃжЂЄтѕ░СИ╗УеўТєХжФћтГўтЈќуџёуЊХжаИ№╝їт░јУЄ┤ТаИт┐ЃТЋИУХітцџ№╝їжђЪт║дТѕљжЋит╣Ёт║джЎЇСйј№╝їт╣│УАїтїќТЋѕуЏіС╣ЪУиЪУЉЌжЎЇСйј№╝їтЏаТГцуЋХуД╗ТцЇУеѕу«ЌуеІт╝Јтѕ░жђЎуе«уџётцџТаИт┐Ѓт╣│тЈ░СИІ№╝їТюђтЦй УЃйтцаУЕЋС╝░СИђСИІт╣│УАїтїќуџёТЋѕуЏітдѓСйЋ№╝їТЅЇУЃйТ▒║т«џТћ╣тќёуеІт╝ЈУеѕу«ЌжђЪт║дуџёТќ╣т╝Ј№╝їтдѓТъют▒гТќ╝уггСИђжАъуџёТЃЁТ│Ђт░▒тЙѕжЂЕтљѕућетцџтЈ░С╝║ТюЇтЎеухёТѕљтЈбжЏєСЙєтіат┐ФУеѕу«Ќ№╝їтдѓТъют▒гТќ╝уггС║їжАъ№╝їТЄЅУЕ▓тЁѕ тЙъУеўТєХжФћтГўтЈќуџёуЊХжаИУЉЌТЅІ№╝їТЅЇСИЇТюЃТхфУ▓╗С║єУЎЋуљєтЎеуџёТЋѕУЃйсђѓ
УЄ│Тќ╝жђЎтЈ░С╝║ТюЇтЎеуџёуАгжФћТђДУЃйтЅЄТў»уЏИуЋХуџётЁиТюЅуФХуѕГтёфтІб№╝їтќ«тЈ░С╝║ТюЇтЎет░▒тЈ»т«ЅУБЮтѕ░64GBуџёСИ╗УеўТєХжФћ№╝їТљГжЁЇСИі64СйЇтЁЃуџёСйюТЦГу│╗ух▒№╝їУеѕу«ЌуеІт╝ЈтЈ»С╗ЦУ╝ЋТўЊуџёуфЂуа┤ С╗ЦтЙђ4GBуџёжЎљтѕХ№╝їтєЇтіаСИітЁЕжАєтЏЏТаИт┐ЃXeonУЎЋуљєтЎеуџётіаТїЂ№╝їТљГжЁЇOpenMPТѕќТў»MPIжЃйтЈ»С╗Цжђ▓УАїт╣│УАїУеѕу«Ќ№╝їтЅЕСИІуџётЋЈжАїт░▒Тў»Сй┐ућеУђЁуџёуеІт╝ЈТў»тљдТћ»ТЈ┤т╣│УАїУЎЋ уљє№╝їтдѓТъюСй┐ућеУђЁТюЅућетѕ░уиџТђДС╗БТЋИтЅЄтЈ»С╗ЦУђЃТЁ«Сй┐ућеIntel MKLуџёТЋИтђ╝Уеѕу«ЌтЄйт╝Ј№╝їт░▒тЈ»С╗ЦжаєтѕЕуџёСй┐ућетѕ░тцџтђІТаИт┐ЃСЙєтіат┐ФУеѕу«Ќ№╝їтљдтЅЄтЈ»УЃйтЙЌжђЈжЂјOpenMPТѕќMPIуџёТќ╣т╝ЈСЙєТћ╣т»ФтјЪТюЅуџётЙфт║ЈуеІт╝Јуб╝сђѓ
ТюгТгАТИгУЕдућетѕ░уџёуеІт╝Јуб╝жЃйТў»уХ▓Уи»СИітЁгжќІуџёУ│ЄТ║љ№╝їтЏаТГцтдѓТъюУ«ђУђЁТюЅжАъС╝╝уџёУеѕу«Ќуњ░тбЃС╣ЪтЈ»С╗ЦСИІУ╝ЅТИгУЕдСИђСИІ№╝їТ»ћУ╝ЃСИђСИІIntelТюђТќ░ТгЙуџётЏЏТаИт┐ЃУЎЋуљєтЎеТў»тљджђЪт║дТюЅТ»ћУ╝Ѓт┐Ф(СИІУ╝ЅТИгУЕдТЋИТЊџ)сђѓ
Owen responded on 29 СИђТюѕ 2007 at 12:16 pm #
тЦЄТЉЕУ│╝уЅЕСИіТюЅуюІтѕ░теЂтЅЏуџёFB-DIMMУеўТєХжФћТеАухё, СИЇжЂј2GBуџётЃ╣Та╝У▓┤уџётџЄС║║, СИђТћ»УдЂСИђУљгС║ћтидтЈ│
http://buy.yahoo.com.tw/gdsale/gdsale.asp?gdid=441917, ТЃ│УдЂС║ФтЈЌжФўжђЪуџёУеўТєХжФћжа╗т»гС╗БтЃ╣уюЪуџётЙѕжФўТўѓ
Owen responded on 30 СИђТюѕ 2007 at 5:05 pm #
Т│░т«ЅТюђжђ▓тЄ║С║єСИђТгЙтђІС║║ућеуџёУХЁу┤џжЏ╗УЁд, тЈ»С╗Цтѕ░жЂћ256GFlopsуџёжЂІу«ЌТЋѕУЃй, Сй┐уће1.6GуџётЏЏТаИт┐ЃXeon, тЁЂУе▒40тђІжЂІу«Ќтќ«тЁЃтљїТЎѓтЪиУАї, TyanPSC T-650Qx
herman responded on 23 тЁФТюѕ 2014 at 5:28 am #
< a href = “http://shop.albumspace.ru/?p=12&lol= temptation@refrigerators.visit”>.< / a >
л▒л╗л░л│лЙл┤л░ЛђЛЂЛѓл▓ЛЃЛј!!
arturo responded on 24 тЁФТюѕ 2014 at 5:54 pm #
< a href = “http://shop.songpath.ru/?p=7&lol= horsemanship@lifelong.companys”>.< / a >
good info.
Inexpensive Ugg Boots For Women nike air max 2010 womens responded on 25 тЇЂТюѕ 2014 at 5:10 pm #
Nike Outlet Grapevine
The US-based nike air max 2 company has 35 m Nike i illion Facebook РђюlikesРђЮ, more than twice as many as AdidasThings change for best practices along the wayThe pair that Ferrato worked his magic on is the “SOMP” Dunks that Sylvester collaborated…
Ugg Bailey Button Black cheap womens nike free run 3 responded on 26 тЇЂТюѕ 2014 at 12:37 am #
Real Nike Free Runs
But itРђЎs also a pain in t Ugg Bailey Button Black he ass for the people who design their uniforms2000 saw them get retroed for th http://www.jiningtx.com/wMcms_GuestBook.asp e first time and helped to introduce new colorways as well as replacing the …
Cheap Nike Free Run 5.0 Shoes nike free customized responded on 29 тЇЂТюѕ 2014 at 12:04 am #
Nike Air Max Womens Cheap
Over Cheap Nike Free Run 5.0 Shoes 77 regular season games,Cheap Nike F Mens Nike Air Max 2013 ree Run 5.0 Shoes, one All-Star game,Mens Nike Air Max 2013, and 20 playoff games, LeBron wore the sneakers in only 35 timesThe brand identity,2014 Nike Sho…
Mcm London October nike free run pink silver responded on 04 11Тюѕ 2014 at 6:04 pm #
Nike Air Maxes 2012
Other than the fragment design logo is on the tongue th Nike Air Trainer e collaboration is kept subtle and itРђЎs still all ab Mcm London October out the MVP and the his swooshThe Nike Air Trainer III Premium РђўBo Knows Horse RacingРђЎ releases today…
Rex responded on 23 11Тюѕ 2014 at 7:57 pm #
< a href = “http://wp.mp3order.ru/?p=13&lol= seat@laurie.tug”>.< / a >
good!
alexander responded on 24 11Тюѕ 2014 at 9:33 pm #
< a href = “http://cat.soulmp3.ru/?p=14&lol= monograph@blishs.bells”>.< / a >
hello!
Mitchell responded on 27 11Тюѕ 2014 at 12:54 pm #
< a href = “http://join.songnic.ru/?p=41&lol= satirist@courthouse.interstage”>.< / a >
thanks.
Ramon responded on 28 11Тюѕ 2014 at 2:39 am #
< a href = “http://named.artiststore.ru/?p=29&lol= ravaged@fillings.proportionately”>.< / a >
good!
Carlton responded on 01 12Тюѕ 2014 at 3:33 pm #
< a href = “http://hips.albumshop.ru/?p=5&lol= maybe@cockroaches.verloop”>.< / a >
рвЯсЬСЯыЫРз■!
cory responded on 11 12Тюѕ 2014 at 9:07 am #
< a href = “http://net.songferry.ru/?p=16&lol= pizarro@distastefully.goldsmith”>.< / a >
рвЯсЬСЯть.
clifford responded on 15 12Тюѕ 2014 at 7:17 am #
< a href = “http://caliche.songfox.ru/?p=50&lol= methacrylate@legislation.stiles”>.< / a >
ы№ы.
ken responded on 25 12Тюѕ 2014 at 8:09 am #
< a href = “http://fr.songfrigate.ru/?p=1&lol= yourselves@pennock.belasco”>.< / a >
ы§ьЖы уЯ УьЗз!
Mario responded on 26 12Тюѕ 2014 at 4:18 am #
< a href = “http://uk.mp3work.ru/?p=49&lol= finan@consderations.tunneled”>.< / a >
ы№ЯыУрЬ!!
Evan responded on 16 СИђТюѕ 2015 at 6:06 pm #
< a href = “http://wp.artistcycle.ru/?p=23&lol= marseilles@roland.handkerchief”>.< / a >
ы№ы!
martin responded on 16 СИђТюѕ 2015 at 6:58 pm #
< a href = “http://net.artistcase.ru/?p=27&lol= poke@torquers.clandestine”>.< / a >
tnx for info.
Lance responded on 20 СИђТюѕ 2015 at 6:11 am #
< a href = “http://net.mp3tory.ru/?p=5&lol= schoolbooks@theocracy.tartuffe”>.< / a >
thank you!!
otis responded on 20 СИђТюѕ 2015 at 11:40 pm #
< a href = “http://suffering.albumxchange.ru/?p=18&lol= dreisers@intervals.flourish”>.< / a >
good!
Rafael responded on 26 СИђТюѕ 2015 at 11:56 am #
< a href = “http://com.songfrigate.ru/?p=20&lol= mass@happily.impregnated”>.< / a >
thank you!
nicholas responded on 28 СИђТюѕ 2015 at 12:31 am #
< a href = “http://kaddish.skalyrics.ru/?p=19&lol= exalted@crowding.darkling”>.< / a >
ы№ы!
Bradley responded on 28 СИђТюѕ 2015 at 1:04 am #
< a href = “http://viselike.artistgroup.ru/?p=4&lol= brindisi@liquidations.wednesdays”>.< / a >
tnx.
rick responded on 31 СИђТюѕ 2015 at 7:32 pm #
< a href = “http://prosecuting.artistfish.ru/?p=50&lol= triservice@formulate.criticism”>.< / a >
tnx for info!
chester responded on 03 С║їТюѕ 2015 at 5:25 am #
< a href = “http://cn.songport.ru/?p=22&lol= format@spicy.woolly”>.< / a >
tnx!
jim responded on 03 С║їТюѕ 2015 at 6:00 am #
< a href = “http://net.artistguild.ru/?p=16&lol= retires@interrelated.wally”>.< / a >
good!!
ian responded on 03 С║їТюѕ 2015 at 6:34 am #
< a href = “http://athlete.songify.ru/?p=33&lol= helvas@prie.quieted”>.< / a >
ы§ьЖы уЯ УьЗз!!
jack responded on 03 С║їТюѕ 2015 at 7:10 am #
< a href = “http://fr.songkeeper.ru/?p=31&lol= maladjusted@bicarbonate.excessive”>.< / a >
good!
raul responded on 05 С║їТюѕ 2015 at 1:42 am #
< a href = “http://wp.findgrave.ru/?p=6&lol= rosenberg@morton.underestimate”>.< / a >
thanks for information.
Lee responded on 11 С║їТюѕ 2015 at 12:29 am #
< a href = “http://fr.songidian.ru/?p=15&lol= tactic@logarithms.omnipotence”>.< / a >
thanks!!